Сложные системы, синергетика и теория целостности

А.П. Хускивадзе

Аннотация

В статье дается краткий сравнительный анализ современных представлений синергетики и теории целостности. Показано, что синергетическое видение устройства – конституции – мира является методологической основой теории целостности.

Статья представляет интерес для специалистов, изучающих сложные – большие – системы, какими являются живые организмы, современные летательные аппараты, атомные станций и т.д.

Ключевые слова: сложная система, живой организм, синергетика, целостность, принятие решения.

Словосочетание «Сложные - большие - системы» особенно интенсивно стало употребляться с начала 60 -ых годов прошлого столетия [1-8]. Позже предпочтение было отдано термину «синергетика», введенному профессором Штутггартского университета и директором Института теоретической физики и синергетики Германом Хакеном [9-12]. Этот термин Г. Хакеном был введен для обозначения науки, изучающей процессы самоорганизации в таких, казалось бы, совершенно не имеющих между собой ничего общего сложных системах, какими являются лазер и мозг человека. В таком понимании с синергетикой связаны модели и методы теории нелинейных колебаний (А Пуанкаре, И. Андронов), теории катастроф (Р.Том), теории хаоса (В. Арнольд), теории диссипативных структур (И.П. Пригожин) и фрактальной геометрии (Б. Мандельброт) [13].

В настоящее время под синергетикой понимают междисциплинарное направление современного точного естествознания. Она анализирует научные идеи, методы и модели сложного поведения и изучает проблемы междисциплинарного диалога, выявляет особенности современных сложных ситуаций и сопоставляет их с соответствующими научными точками зрения о сложных системах, хаосе, фракталах и т.д. (Ж. Диотар, Ж. Делез и Ф. Гватари, И.Р. Пригожин и И. Стенгерс, У. Матурана, В.И. Аршинов, Н. Леман).

В последние годы наблюдается стремительный и бурный рост интереса к синергетике. Издаются солидные монографии, учебники, выходят сотни статей, проводятся национальные и международные конференции и т.д. Идеи синергетики проникают во все области знания, начиная от физики и химии и кончая лингвистикой [14-37].

Системы, изучаемые синергетикой, состоят из большого числа частей, взаимодействующих между собой сложным образом, но согласованно. Слово «синергетика» и означает «совместное действие», подчеркивая согласованность функционирования частей, отражающуюся в поведении системы как целого» [16].

Теорией целостности [38] изучаются как сложные, так и простые системы. Точнее, в теории целостности предполагается, что любая система является одновременно и простой, и сложной. Все зависит от уровня детализации ее рассмотрения. Система, рассмотренная достаточно подробно, является сложной системой [2].

Отличие синергетического взгляда от традиционного «состоит в переходе от исследования простых систем к сложным, от закрытых к открытым, от линейности к нелинейности, от рассмотрения равновесия и процессов вблизи равновесия к…нестабильности, к изучению того, что происходит в дали от равновесия» [15].

Теория целостности не делит системы на открытые и закрытые, линейные и нелинейные. Она исходит из того, что каждая система является одновременно и открытой, и закрытой, и линейной, и нелинейной.

Системы, составляющие предмет изучения синергетики, могут быть самой различной природы и специально изучаться соответствующими науками [16]. Те же системы являются предметом изучения теории целостности.

Синергетику интересуют общие закономерности эволюции (развития во времени) систем любой природы [16]. Закономерности гармонии природы, изучаемые теорией целостности, как раз и являются общими закономерностями эволюции систем любой природы.

Отрешаясь от специфической природы систем, синергетика, как и теория целостности, обретает способность описывать эволюцию систем на интернациональном языке, одинаково доступном исследователям из различных областей знания. В теории целостности в качестве такого языка служит язык, использующий понятийный аппарат математической статистики и теории множеств. Сегодня этот понятийный аппарат одинаково доступен ученым всех без исключения областей знания.

Синергетика, наводит мост через брешь, разделяющую редукционистский подход от холистического [16]. Теория целостности, исходя из того, что каждая материальная реальность (МР)S является одновременно и целостной системой, и элементом целостной системы более высокого уровня, делает то же самое. Понятием «Материальная реальность» в теории целостности обозначают все то, что возникает и исчезает и, следовательно, имеет вполне определенные время возникновения и время исчезновения.

В синергетике сжатие информации достигают тем что, вместе большого числа факторов, от которых зависит состояние системы (так называемых компонентов вектора состояния), рассматривают немного численные параметры порядка. Так именуют величины, от которых зависят компоненты вектора состояния системы и которые, в свою очередь, влияют на параметры порядка [16]. В итоге, сложная «многомерная динамика системы описывается небольшим числом параметров порядка, демонстрируя простое поведение. Согласно принципу подчинения синергетики, параметры порядка детерминируют поведение отдельных частей или элементов системы. Преимущество описания поведения сложных систем путем определения параметров порядка и применения принципа подчинения состоит в существенной редукции степеней свободы, в огромном сжатии информации.

Возможно решение как прямой, так и обратной задачи: определение параметров порядка сложной системы и, наоборот, восстановление поведения этой системы по известным параметрам порядка» [15].

В теории целостности, вместо параметров порядка, вводятся скалярные величины g и P, служащие аналитической и вероятностной интегральными характеристиками согласованности действий частей МР S как целого. Точнее, через P обозначена вероятность фактического познания истины в МР S в момент времени t = t₀: (t₁ ≤ t₀ ≤ t₂), а величина g служит мерой проявления, так называемого, единого интегративного качества МР S в момент времени t = t₀,

где

t₁ – время возникновения МР S;

t₂ – время исчезновения МР S.

Словосочетание «Единое интегративное качество» в наше поле зрения впервые попало из работ советского философа В.Г. Афанасьева. Под этим им понимается качество, проявляемое МР S и ее частями совместно и только совместно [39- 40].

То, что единое интегративное качество (ЕИК) в живой природе в действительности существует, впервые было установлено Канадским ученым Г. Селье [41- 42], а В.Г. Афанасьев показал, что ЕИК является общим качеством материальных реальностей как живой, так и неживой природы.

Величины g и P, как интегральные характеристики одной и той же МР S, являются между собой тесно взаимосвязанными. Для того, чтобы выяснять, в чем это взаимосвязь выражается, в первую очередь, необходимо ввести понятие «Генеральная совокупность первичных показателей состояния системы». А для этого, со своей стороны, прежде всего, должно быть уточнено, что следует понять под термином «Система». Дело в том, что в настоящее время все еще продолжаются споры о том, что следует понять под этим термином [26–28, 43-49]. «К понятию системы – пишет Н. Луман – можно подходить по разному. Например, в смысле Аристотеля: система - это совокупность частей. Или в биологическом смысле: система - это целостность, отличная от окружающей среды. Кибернетика пытается совместить эти подходы: с одной стороны, система – это целостность, ограниченная от внешней среды, с другой стороны, система – это то, что имеет внутреннюю структуру» [28].

Таким образом, понятие «Система» может иметь различные толкования в зависимости от решаемых задач. Однако, если задача самая общая, - а задача поиска самых общих закономерностей природы является самой общей задачей, - то и понятие «Система» должно быть самое общее, т.е. оно должно иметь один и тот смысл для материальных реальностей любой природы.

Ниже, формализуя понятие «Система», мы исходим из нашей главной задачи: - найти и описать самые общие закономерности гармонии природы.

Пусть

A_j ⊂ A; j = 1..n

- непустые конечные множества материальных реальностей, а

H_j; j = 1..n

- непустые конечные множества отношений такие, что для каждой пары

S_j = < A_j, H_j > ; j = j₀; j₀ = 1..n

имеет место

S_j = S_j0 Û  y_j = y_j0 Î Y,

а для пары S = < A, H > выполняется условие

S = S₀ Û  Y = Y₀ ,

т.е. вообще имеют место

S = S₀ Û  Y = Y₀ и S_j = S_j0 Û  y_j = y_j0 для всех j = 1..n , (1)

где S₀, Y₀, S_j0 и y_j0 являются фиксированными значениями S, Y, S_j и y_j соответственно.

Определение 1

Пусть, имеет место (1) и при этом

2 £ n < ¥

и (2)

S = S₀ Û  S_j = S_j0 для всех j = 1.. n

Тогда и только тогда говорят, что пара S является системой элементов

S_j; j = 1..n.

О каждой паре S_j говорят, что она является j –ой функциональной частью системы S.

Если n = 1, т.е. имеет место: S = S₁, то о паре S говорят, что она является элементом системы более высокого уровня.

О каждой паре S_j говорят также, что она является j –им функциональным элементом системы S

Функциональные элементы системы, в отличие от ее анатомических частей, являются между собой тесно переплетенными, подобно тому, как переплетены между собой физиологические системы живого организма.

Рассмотрение МР S, как системы, представляющей собой единство определенных функциональных элементов, имеет принципиальное значение. Дело в том, что «функция – первична, а структура – вторична. Структуры могут меняться, а функции остаются. Задав вопрос о функциях первым, только потом надо переходит к структурам» [28].

Замена системы функциональных элементов МР S другой системой функциональных элементов равносильна замене самой этой материальной реальности другой материальной реальностью.

Иными словами, в течение всего времени от t₁ до t₂ система функциональных элементов для каждой МР S является одной единственной, т.е. вполне определенной. Этого нельзя сказать о системах, составленных анатомическими частями МР S. Этих последних имеется столько, сколько имеется уровней детализации рассмотрения МР S.

Определение 2

Пусть, пара S является системой, т.е. выполняется совокупность условий (1) и (2).

Тогда и только тогда говорят, что множество

y_j; j = 1..n (3)

является генеральной совокупностью первичных показателей состояния системы S .

В физике и синергетике о величинах (3) говорят, что они являются компонентами вектора состояния системы S.

Вообще

g = g (g _j; j = 1..n)

и (4)

P = P(P_j; j = 1..n),

где

g _j -мера проявления ЕИК j –ым функциональным элементом МР S в момент времени

t = t₀;

P_j – вероятность познания истины j –ым функциональным элементом МР S в момент времени t = t₀.

Пусть b_jl - результат l -го измерения j – го компонента вектора состояния МР S в момент времени t_j:

t_j1 ≤ t_j ≤ t₀,

где

t_j1 – начало интервала времени, когда

ê b_jl - b_j(t₀) ê < D _j(П) для всех l = 1.. N_j1; (5)

b_j(t₀) – значение b_jl при t_j = t₀;

D _j(П) –абсолютная погрешность измерительного прибора j – го компонента вектора состояния МР S.

В случаях, когда выполняется условие (5) говорят, что j – ый компонент вектора состояния МР S в течение времени от t_j1 до t₀ находится в одном и том же состоянии.

В итоге, совокупность

B_j = {b_jl ; l = 1..N_j1}; j = 1..n

служит характеристикой фактического состояния МР S в момент времени t_j = t₀.

Вообще

1 ≤ N_j1; j = 1..n

Обозначим

M_j1 = и S_j1 = (6)

Можно показать, что

g _j = g _j(M_j1, S_j1, N_j1; j = 1..n; j = 1..n) и P_j = P_j(M_j1, S_j1, N_j1; j = 1..n)

или, с учетом (3),

g _j = ¦ _j(b_jl ; l = 1..N_j1; j = 1..n) и P_j = f _j(b_jl ; l = 1..N_j1; j = 1..n) (7)

Таким образом, как каждая g _j, так и каждая P_j, определяется всей совокупностью исходных данных

b_jl ; l = 1..N_j1; j = 1..n (8)

В этом и проявляется целостность системы S.

В итоге, согласно (4) и (7) имеем

g = ¦ (b_jl ; l = 1..N_j1; j = 1..n) и P = f (b_jl ; l = 1..N_j1; j = 1..n) (9)

Алгоритм определения величин g и P по известным данным (5) приведен в [38].

Синергетика исходит из того, что эффективные решения могут быть найдены в любых условиях [17, с.2]. Тем самым , она признает, что каждая система имеет свою вполне определенную возможную среду наиболее благоприятного существования – «конус аттрактора» Существования такой среды признается и теорией целостности. Более того, она предлагает способ воссоздания этой среды. Этот способ реализован в виде программы «Универсальный советчик принимающего решения (УСПР)» [38].

Обозначим через H среду существования МР S. Пусть H₀ значение H такое, что

H = H₀ при t = t₀

Говорят, что условия существования j –го функционального элемента МР S при H = H₀ являются наиболее благоприятными, если

P_i = max{P_j; j= 1..n} (10)

Пусть

M_j0^*, S_j0^* и N_j0^*; j = 1..n (11)

- значения

M_j1, S_j1 и N_j1; j = 1..n (12)

такие, что

M_j1 = M_j0^*; S_j1 = S_j0^* и N_j1 = N_j0^* при P_j = P_i для всех j = 1..n

Так как вообще

P_i ≥ P_j; j= 1..n,

то, казалось бы, всегда должно иметь место

P^* ≥ P; j= 1..n, (13)

где

P^*- значение P такое, что

P = P^* Û M_j1 = M_j0^*; S_j1 = S_j0^* и N_j1 = N_j0^* для всех j = 1..n

В действительности, однако, неравенство (13) будет выполняться, если внешняя составляющая среды существования МР S при замене совокупности (12) совокупностью (11), будет сохраняться неизменной.

Как правило, внешняя составляющая среды существования МР S меняется медленно. Так, внешняя составляющая среды существования человека сохраняется практически неизменной сотни тысяч лет.

В итоге, условие (13) практически все же выполняется всегда.

Итак, зная совокупность исходных данных (8), можно однозначно определить величины

g _j и P_j ; j = 1..n

и, в конечном счете, величины g и P. А зная эти величины и пользуясь программой УСПР, со своей стороны, можно воссоздать такую среду существования МР S, чтобы в момент времени

t_j = t₀ + D t; D t > 0

имело место

g (t₀ + D t) ≥ g и P(t₀ + D t) ≥ P

В итоге, как и в синергетике, и тут возможно решение как прямой, так и обратной задачи: определение интегральных характеристик сложной системы по совокупности исходных данных и, наоборот, воссоздание новой совокупности исходных данных по известным интегральным характеристикам.

Таким образом, как в синергетике, так и в теории целостности, реализуется так называемый «феномен циклической причинности» [15, с.3]: поведением всей совокупности элементов определяется поведение системы как целого и, наоборот, поведением системы как целого, определяется поведение элементов, ее составляющих.

Если конус аттрактора таков, что имеет место P = P₀, то говорят, что МР S при t = t₀ находится в нормальном состоянии и пишут: g = 1, а точнее полагают, что

g = 1 Û P = P₀, (14)

где

P₀ – вероятностный предел познания истины в МР S при t = t₀.

В том случае, когда МР S находится в нормальном состоянии, пишут:

M_j0 = M_j0^*; S_j0 = S_j0^* и N_j0 = N_j0^* для всех j = 1..n,

где

M_j0 ; S_j0 и N_j0; j = 1..n

– совокупность первичных характеристик нормального состояния МР S при t = t₀.

Вообще

ê M_j0 = M_j0^*ê ≥ 0; ê S_j0 = S_j0^*ê ≥ 0 и ê N_j0 = N_j0^*ê ≥ 0; j = 1..n

(1 – P) ≤ g ≤ 1 (15)

0.5 ≤ P ≤ P₀ ≤ P₀(S) ê <1,

где

P₀(S) – наибольшее возможное значение P₀ для МР S:

P₀ ≤ P₀(S) при t₁ ≤ t₀ ≤ t₂

При этом

P₀ ® P₀(S) при t₁ ≤ t₀ ≤ t₁₀

P₀ = P₀(S) при t₁₀ ≤ t₀ ≤ t₂₀ (16)

P₀ ® 0.5 при t₂₀ ≤ t₀ ≤ t₂,

где

t₁₀ и t₂₀

- начало и конец периода расцвета МР S.

Так как вообще

P ≤ P_0,

в случаях, когда

P₀ = 0.5,

имеет место

P = P₀ = 0.5 (17)

В таких случаях МР S одновременно и находится и не находится в нормальном состоянии.

О состоянии МР S, когда выполняется условие (17), можно говорить, что оно является неопределенным состоянием МР S. Вне области (t₁, t₂) МР S всегда находится в неопределенном состоянии.

Пусть

a_s; s = 1..m; m ≥ 2 (18)

множество материальных реальностей такое, что

= A и = Æ (19)

Определение 3

Пусть

h_s ¹ Æ ; s = 1..m

- множества отношений, заданных на множества (18) такие, что качество функционирования каждой материальной реальности

s = < a_s, h_s>; s = s₀; s₀ = 1..m (20)

описывается той же совокупностью первичных показателей, какою описывается качество функционирования всей системы S, т.е. имеет место

Y_s = Y; s = 1.. m, (21)

где

Y_s - генеральная совокупность первичных показателей качества функционирования МР s.

Тогда и только тогда о материальных реальностях

. s = 1.. m (22)

говорят, что они являются анатомическими элементами системы S.

Анатомические элементы системы S, согласно (19), не пересекаются между собой. Этим они принципиально отличаются от функциональных элементов этой системы.

Примерами анатомических элементов служат органы тела человека.

То, что качество функционирования каждой МР s описывается совокупностью показателей Y, указывает на то, что эта МР, со своей стороны, тоже является системой функциональных элементов, аналогичных функциональным элементам системы S.

Пусть

M_j1(s); S_j1(s); N_j1(s); j = 1..n (23)

- значения величин.

M_j1; S_j1; N_j1; d _j и τ_j j = 1..n

такие, что

M_j1(s) = M_j1; S_j1(s) = S_j1; N_j1(s) = N_j1 при s = S; j = 1..n (24)

О величинах (23) говорят, что они являются характеристиками фактического состояния системы s при t = t₀.

Пусть, существует система s = 0 такая, что

M_j1(s) = M_j1(0); S_j1(s) = S_j1(0) и N_j1(s) = N_j1(0) при s = 0, (25)

где

M_j1(0) = ; S_j1(0) = и N_j1(0) = ; j = 1..n (26)

О системе s = 0 говорят, что она является типичным представителем (ТП) множества систем (22). Соответственно о величинах

M_j1(0); S_j1(0) и N_j1(0); j = 1..n (27)

говорят, что они являются характеристиками фактического состояния типичного представителя множества систем (22).

Система s = 0, как ТП совокупности систем (22), во-первых, является системой того же уровня, что и системы (22). Следовательно, качество функционирования этой системы, в отличие от качества функционирования системы S, сопоставимо с качеством функционирования любой системы из совокупности систем (22).

Во- вторых, система s = 0, как ТП совокупности систем (22), по сути дела, служит «лицом» всей большой системы S. Следовательно, по качеству функционирования системы s = 0 вполне можно судить о качестве функционирования самой системы S.

В итоге, изучая совокупность систем

s = 0.. m (28)

тем самым, по сути дела, мы будем изучать всю саму систему S.

Принимая во внимание выше изложенное, далее, вместо S, мы будем изучать именно совокупность систем (28).

Пусть

M_j0(0); S_j0(0) и N_j0(0); j = 1..n (29)

- значения величин

M_j1(0); S_j1(0) и N_j1(0); j = 1..n

такие, что

M_j1(0) = M_j0(0); S_j1(0) = S_j0(0) и N_j1(0) = N_j0(0) при P = P₀; j = 1..n (30)

О величинах (29) говорят, что они с вероятностью P служат статистическими характеристиками нормального состояния системы S при t = t₀. При этом, арифметические средние

M_j0(0); j = 1..n (31)

являются точечными статистическими нормами величин (3) для системы S при t = t₀. Эти арифметические средние при t = t₀ одновременно являются точечными статистическими нормами величин (3) и для всех систем (28).

Обозначим

A_j(0) = [M_j0(0) - D _j, M_j0(0) + D _j], (32)

где

D _j –системная единица измерения величины y_j Î Y:

D _j = (1 – P) M_j0(0) ≥ D _j(П)

Об области A_j(0) говорят, что она является областью статистической нормы систем (28) в широком смысле. Одновременно она является областью статистической нормы величины y_j Î Y для системы S при t = t₀.

Обозначим

M_j0(s) = M_j1(s) при M_j1(s) Î A_j(0)

и (33)

M_j0(s) = M_j0(0) при M_j1(s) Ï A_j(0),

О величинах (33) говорят, что они с вероятностью P служат индивидуальными характеристиками нормального состояния системы s при t = t₀. А о величинах

M_j0(s); j = 1..n (34)

говорят, что они являются точечными индивидуальными нормами величин (3) для системы (s) при t = t₀.

Вообще

P = P₀ Û M_j0(s) Î A_j(0) для всех j = 1..n

Все значения величины M_j1(s), для которых имеет место M_j1(s) Î A_j(0), согласно (32) и (33), являются практически неразличимыми от M_j0(0). Ввиду этого, казалось бы, вполне достаточно введение A_j(0) и нет необходимости введения M_j0(s). На самом деле, однако, введение M_j0(s) необходимо по следующим причинам.

1.Величина M_j0(s), являясь вполне определенным числовым значением y_j Î Y, служит объективной характеристикой состояния j –го элемента системы s в той мере, в какой при M_j1(s) Î A_j(0) таковой служит величина M_j1(s).

2. Величина M_j0(s), как и величина M_j1(s), позволяет оперировать высшей шкалой измерений – шкалой отношений.

Иными словами, к величине M_j0(s) применимы все арифметические операции, чего нельзя сказать об области A_j(0).

3. Вообще для точечных индивидуальных норм, как естественных глобальных оптимумов, имеет место

M_j1(s) = M_j0(s) Û M_i1(s) = M_i0(s) для всех j,i = 1..n (35)

Зависимость (35) справедлива только для глобальных оптимумов и только для них.

Следовательно, если мы ограничимся рассмотрением одних областей

A_j(0); j = 1..n,

то, тем самым, мы утеряем доступ к зависимости (35).

Итак, введение величин (34) нам позволяет:

1. Оперировать всеми арифметическими действиями.

2. Считаться с объективной реальностью, выраженной зависимостью (35).

Пусть P^*- заданная вероятность репрезентативности выборок, с помощью которых величины (24) установлены.

Обозначим

d_j1(s) = S_j1(0); j = 1..n; s = 0..m

t_j1(s) = t (P^*, (N_j1(0) – 1)); j = 1..n; s = 0..m

s _j1(s) = d_j1(0) t_j1(0); j = 1..n; s = 0..m

где

t_j1(s) - критическое значение критерия Стьюдента при доверительной вероятности P^* и степени свободы (N_j1(s) – 1 ).

Пусть

s _j0(0); j = 1..n

- значения

s _j1(0); j = 1..n

такие, что

s _j1(0) = s _j0(0) при P = P₀; j = 1..n (36)

Обозначим

Y_j(0) = [M_j0(0) - s _j1(0), M_j0(0) + s _j1(0)) ; j = 1..n

Можно показать, что вообще [38]:

A_j(0) Ê Y_j(0); j = 1..n

Об области Y_j(0) можно говорить, что она является областью статистической нормы системы S в общепринятом смысле.

В настоящее время в биологии и медицине оперируют данными

M_j0(0) ± s _j1(0)); j = 1..n,

которые устанавливают по результатам обследования однородной группы практически здоровых особей в состоянии покоя.

В таблице 1 эти данные приведены в столбце 2. Они установлены по результатам обследования состояния сердца практически здоровых людей в покое. В столбцах 3 и 4 таблицы 1 приведены данные

M_j1(s) ± s _j1(s); j = 1..n; s = 1, 2

Таблица 1. Характеристики состояния правых отделов сердца у здоровых людей и больных хронической обструктивной болезнью легких.

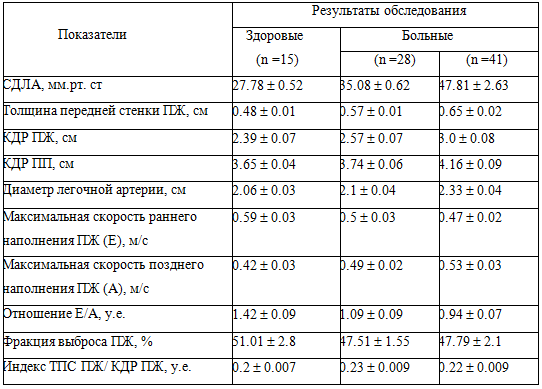
Они установлены по результатам обследования состояния сердца двух групп больных в покое. Эти группы больных страдают одним и тем заболеванием: - хронической обструктивной болезнью сердца. Друг от друга эти группы отличаются лишь по тяжести заболевания. Заимствованы все эти данные из [50].

В целом данные таблицы 1 служат статистической характеристикой фактического состояния системы S, составленной из выше упомянутых трех групп людей. В этой системе в наилучшем – нормальном - состоянии, как указывалось выше, находятся люди контрольной группы. Следовательно, точечные статистические нормы этих людей должны служить в качестве точечных статистических норм и для всей системы S. Так ли это на самом деле?

Для выяснения этого вопроса все данные таблицы 1 были совместно обработаны с помощью УСПР. Установленные с помощью УСПР точечные статистические нормы системы S приведены в столбце 3 таблицы 2. А в столбце 2 таблицы 2 приведены точечные статистические нормы, переписанные из столбца 2 таблицы 1.

Таблица 2. Точечные статистические нормы состояния правых отделов сердца женщин

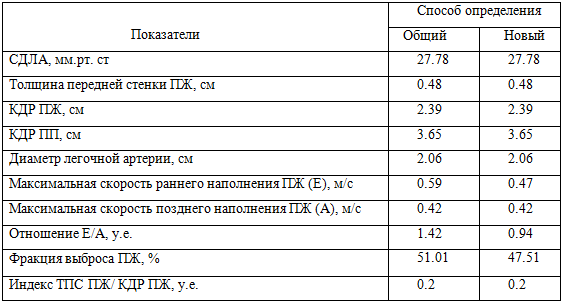
Как видно из таблицы 2, точечные статистические нормы 7 показателей, установленные с помощью УСПР, совпадают с точечными статистическими нормами, установленными общеизвестным способом, а для трех показателей имеются некоторые различия.

Аналогичными являются результаты обработки большого количества других статистических материалов, собранных специалистами в различных областях медицинской науки и биологии.

То, что для некоторых показателей имеются различия, отнюдь не говорит о недостатках настоящего способа. Это различие является следствием ошибок, допущенных при применении общеизвестного способа. Точнее, оно вызвано ошибками, допущенными при отборе контингента практически здоровых людей.

Дело в том, что отбор контингента практически здоровых людей является важнейшим составляющим общеизвестного способа установления статистических норм, а новый способ сам определяет, какие данные служат статистическими нормами, т.е.

характеристиками здоровых людей, и какие – нет. Если, конечно, среди обрабатываемых данных содержатся данные о здоровых людях. Этот способ является единым правилом совместной обработки данных и, если с его помощью для одних показателей устанавливаются точечные статистические нормы, то эти нормы будут установлены и для других показателей. Так, что причину различия следует искать именно в общеизвестном, а не в новом способе.

Итак, точечные статистические нормы (31), установленные с помощью УСПР,

полностью совпадают с точечными статистическими нормами, корректно установленными общепринятым способом. Это служит практическим подтверждением объективности закономерностей гармонии природы, лежащих в основе алгоритма работы программы УСПР и, в конечном счете, указывает на плодотворность теории целостности.

В заключение следует обратить внимание на следующее.

В медицине и биологии величины (31), как указывалось выше, устанавливают по результатам обследования определенной выборки здоровых особей. А с помощью УСПР эти величины, как и остальные производные величины, приведенные выше, устанавливаются по результатам обследования фактического состояния конкретного живого организма, который может быть здоровым, а может и не быть.

Если организм является здоровым, то величины (31), как было показано выше, будут совпадать с точечными статистическими нормами, корректно установленными общеизвестным способом. Во всех других случаях эти величины будут служить в качестве тактических точечных статистических норм, т.е. они будут являться ориентирами на данном этапе лечения больного.

Многие современные ученые (Р,М, Баевский, Э.В. Минаков, М.А. Гайдес и др.),. считают, что опираясь на тактические нормы, можно существенно повысить эффективность лечения больных.

Эффективность лечения станет еще более высокой, если оперировать не статистическими, а индивидуальными нормами каждого больного. Для этого достаточно чтобы, врачи - практики научились вносить результаты обследования больного в компьютер, снабженный программой УСПР. Определение индивидуальных норм, и вообще оценка состояния больного, будет производиться компьютером. За врачом останется главное: подобрать способы воздействия на организм больного, обеспечивающий реализацию выработанных компьютером рекомендаций.

Выводы.

1. Синергетикой изучается системы, состоящие из большого количества частей. А количество частей любой системы является тем большей, чем подробнее эта система рассматривается. Система, рассмотренная достаточно подробно, является сложной системой.

В итоге, и синергетикой, и теорией целостности изучаются одни и те же системы, именуемые как сложные – большие – системы. Однако, теория целостности, в отличие от синергетики, не делает акцента на сложности систем, а исходит из того, что каждая система является одновременно как простой, так и сложной.

2. Как синергетика, так и теория целостности ищут самые общие закономерности природы. Следовательно, и синергетика, и теория целостности исходят из того, что существуют закономерности, которыми управляются любые материальные реальности, независимо от их конкретной природы. Это означает, что видение устройства – конституции – мира теорией целостности таково же, как в синергетике. Так что, вполне можно говорить, что синергетическое видение устройства мира служит методологической основой теории целостности.

3.Теория целостности исходит из того, что каждая система, как единство противоположностей, является одновременно и открытой и закрытой; линейной и нелинейной; стохастической и детерминированной. По этой причине она не делит системы на открытые и закрытые, линейные и нелинейные, стохастические и детерминированные. Как следствие этого: теория целостности не может оперировать и не оперирует специфическими математическими средствами нелинейной динамики, теории хаоса, теории катастроф, теории диссипативных структур, фрактальной геометрии и т.д.

Теория целостности, подобно классической физике, просто описывает объективные закономерности природы. Но, в отличие от классической физики, во – первых, она описывает самые общие закономерности природы – закономерности ее гармонии.

Во – вторых, теория целостности не вырабатывает своих специальных понятий. Она пользуется самыми общими понятиями теории множеств и современной математической статистики: открытое множество, закрытое множество, случайная величина, генеральная совокупность, выборка, ошибка выборки, вероятность, среднее арифметическое, доверительный интервал и т.д. Эти понятия являются одинаково употребляемыми во всех сферах современной науки и техники, т.е. они являются самыми общими понятиями, соответствующими по степени общности описываемым ими закономерностям.

4. Самые общие закономерности природы можно было бы описать и на языке отдельных точных наук. Однако, тогда, при выяснении вопроса всеобщности этих закономерностей, понадобилось бы создавать язык – переводчик, так называемый интернациональный язык.

Понятийный аппарат, используемый в теории целостности, по сути дела, и является таким интернациональным - междисциплинарным - языком. Уже одно это дает теории целостности право на существование.

Итак, теорией целостности самые общие закономерности природы описаны на самом общем – междисциплинарном - языке.

5. Закономерности гармонии природы легли в основу способа определения индивидуальных и статистических норм живого организма по результатам обследования его фактического состояния.

Многократные проверочные расчеты показали, что точечные статистические нормы, установленные новым способом, полностью совпадают с точечными статистическими нормами, корректно установленными с помощью общеизвестного способа. Это служит практическим подтверждением объективности закономерностей гармонии природы и, в конечном счете, указывает на плодотворность теории целостности.

Таким образом, есть все основания говорить, что теория целостности является математической реализацией современных синергетических представлений о мироустройстве.

Литература

1.Денисов А.А., Колесников Д.Н. Теория больших систем управления. - Л.:, - Ленинградское отделение энергоиздата. – 1962.

2. Ляпунов А.А., Яблонский С.В. Теоретические проблемы кибернетики. – «Проблемы кибернетики». - № 9. – 1963

3. Ушаков И.А. Эффективность функционирования сложных систем. – Сб. «О надежности сложных технических систем». – М.:, - «Советское радио», - 1966

4. Малиновский А.В. Сложные системы и термодинамика. – Доклад на 2-ой Всесоюзной школе - семинаре по управлению большими системами. – Тбилиси. - 1973

5. Флейшман Б.С. Статистические пределы эффективности сложных систем. – Сб. «Прикладные задачи технической кибернетики». – М.:, - «Советское радио». - 1966

6. Бусленко Б.С. Моделирование сложных систем. – М.:, - «Наука». - 1968

7. Флейшман Б.С. Элементы теории потенциальной эффективности сложных систем. – М.:, - «Советское радио». - 1971

8. Малиновский А.В. Модели совместного функционирования многих целенаправленных элементов. – «Автоматика и телемеханика», - № 11, 12, - 1972

9. Haken H., Graham R. Synergelik – Die Lehre vom Zusammenwirken. 11 Umschau. 1971. vol. 6. S. 191

10.Хакен Г. Синергетика. – М., - Мир.- 1980. – 404 с.

11. Haken H. Principles of Brain Functioning. A Synergetic Approach to Brain Activity. Behavior and Cognition. in, Springer. 1996

12 Хакен Г . Самоорганизующееся общество. // Будущее России в зеркале синергетики. М.: КомКнига, 2006.

13 Данилов Ю.А., Кодомцев Б.Б. Что такое синергетика? Перепечатана из книги: «Нелинейные волны. Самоорганизация». – М., - Наука. - 1983

14 Mainzer K. Thinking in Complexity. The Complex Dynamicsof Matter. Mind. And Mankind. 3 rd rev. Andenlarget ed. Berlin. Springer. 1997

15 Князева Е.Н. Сложные системы и нелинейная динамика в природе и обшестве. ММСФ

16 Данилов Ю.А. Роль и место синергетики в современной науке. – Российский научный центр «Курчатовский институт», - ММСФ

17.Князева Е. Н. Синергетический вызов культуре.- ММСФ

18. Князева Е. Н., Курдюмов С. П. «Основания синергетики. Синергетическое мировидение». М.: КомКнига, 2005. (Изд. 3, доп. М.: ЛИБРОКОМ/УРСС, 2010).

19 Князева Е. Н., Курдюмов С. П. «Основания синергетики. Человек, конструирующий себя и свое будущее». М.: КомКнига, 2006.

20. Князева Е. Н., Курдюмов С. П. Синергетика: нелинейность времени и ландшафты коэволюции. – М., КомКнига, -2007

21. Буданов В.Г. Синергетические стратегии в образовании. – ИФ РАН.- ММСФ

22. Назарян А.И. Модели самоорганизации в науках о человеке и обществе. -ММСФ

23 В.И. Аршинов Постнеклассические практики, конвергирующие (трансформативные) технологии и проблемы коммуникации в сложностностях” - synergia-isa.ru/?p=2991

24 .У. Матурана и Ф. Варела Древо познания. Перевод с англ. Ю.А. Данилова. – М.: Прогресс-Традиция, - 2001. – 224 с.

25 Чарльз Франкос Кто знает, что такое Общая Теория Систем? -http://www.newciv.org/ISSS_Primer/seminar. html

26. Кент Палмер Теория Автопоэтических рефлексивных систем. Перевод с английского Червоткина Р.В. - ММСФ

27. Никлас Луман " Почему необходима "системная теория?" - Terpsta's Luhmann Web Page

28. Никлас Луман " Что такое организация? - Terpsta's Luhmann Web Page

29 Пригожин И. Конец определенности. http://www.edurss.ru/cgi-bin/db.pl?cp=&page=Book&id=1387&lang=Ru&blang=ru&list=Found

30. Пригожин И., Стенгерс И. Порядок из хаоса.- http://www.edurss.ru/cgi-bin/db.pl?cp=&page=Book&id=11743&lang=Ru&blang=ru&list=Found

31. Пригожин И., Стенгерс И. Время. Хаос. Квант . - http://www.edurss.ru/cgi-bin/db.pl?cp=&page=Book&id=12190&lang=Ru&blang=ru&list=Found

32 Пригожин И. От существующего к возникающему. М., -«УРСС». – 2002

33 Николас Г., Пригожин И. Самоорганизация в неравновесных системах. – М., - МИР.- 1979.- 277 с.

34. Гильберт Д. Познание природы и логика  http://vivovoco.nns.ru/VV/PAPERS/NATURE/GILBERT.HTM

35..Р. Витакер (R. Whitaker) Обзор основных понятий теории автопоэзиса

36 Ушаковская Е.Д. О причинах синергетических процессов и эволюции вселенной. – Санкт-Петербург.- НТФ – «Теплофизприбор».- yshakovskaya@inbox.ru.

37 Казанский А. Б . Биосфера, как автопоэтическая система: Биосферный бутстрап, биосферный иммунитет и человеческое общество. – Экогеософский альманах, - Санкт-Петербург, - 2003. - a №3, - c . 5-50.

38 Хускивадзе А.П. Мироустройство. - Medlinks.ru - Медицинская библиотека. - Фундаментальная медицина. - Книги и руководства. – 2010. – 110 с. http://www.medlinks.ru/sections.php?op=listarticles&secid=108

39 Афанасьев В.Г. Системность и общество. – М., Изд-во полит. литературы. – 1980. – 358 с.

40 Афанасьев В.Г. Общество, системность, познание и управление.- М., Изд-во полит. литературы. – 1981

41 Тигранян Р.А. Стресс и его значение для организма. – М., - Наука. – 1966. – 176 с.

42. Сель Г. Стресс без стресса. – М., Прогресс. – 1979. – 123 с.

43. Холл А.Д., Фейджин Р.Э. Определение понятия системы. – Сб. «Исследования по общей теории систем». – М., - Прогресс, - 1969

44. Уемов А.И. Логический анализ системного подхода к объектам и его место среди других методов исследования».- М., - Наука, - 1969

45. Л. Фон Берталанфи Общая теория систем – критический обзор. – Сб. «Исследования по общей теории систем». – М., - Прогресс, - 1969

46. Тода М., Щуфорд Э.Х. Логика систем: введение в формальную теорию структуры. –Сб. «Исследования по общей теории систем». – М., - Прогресс, - 1969

47. Клар И. Абстрактное понятие системы, как методологическое средство. – Сб. «Исследования по общей теории систем». – М., - Прогресс, - 1969

48. Эллис Д., Людвиг Ф. Строгое определение понятия системы. – Сб. «Исследования по общей теории систем». – М., - Прогресс, - 1969

49. Месарович М.Д. Общая теория систем и ее математические основы. – Сб. «Исследования по общей теории систем». – М., - Прогресс, - 1969

50. Карели Н.А., Ребров А.П., Сергеева В.А. Формирование хронического легочного сердца у больных хронической обструктивной болезнью легких // Клиническая физиология кровообращения. – 2007.- №4. – с. 26-34.

11.12.2010

Интересное по этой теме: